Capitulo 01

Aqui, vamos mergulhar no algoritmo que deu origem a toda essa aventura. Sim, estamos falando daquele artigo com título complicado: “Optimized Ensemble Learning Approach with Explainable AI for Improved Heart Disease Prediction”, publicado em junho de 2024. Embora não seja um assunto trivial, com um pouco de esforço e dedicação, você verá que é perfeitamente compreensível e, mais importante, aplicável a problemas reais de negócios.

Entendendo o Contexto

O artigo aborda um problema altamente relevante: a previsão de doenças cardíacas usando aprendizado de máquina. Os autores propõem uma abordagem inovadora, que combina modelos de ensemble otimizados com técnicas de interpretabilidade, com o objetivo não apenas de melhorar a precisão, mas também de entender os fatores que mais influenciam as previsões. Ou seja, não basta saber se uma pessoa tem uma doença cardíaca, é fundamental entender o “porquê” por trás dessa previsão.

E por que isso é importante? Porque, seja na saúde, nos negócios ou em qualquer outro contexto, as previsões baseadas em dados precisam ser confiáveis e explicáveis. E essa combinação de alta performance e interpretabilidade não só melhora os resultados, mas também garante confiança nas decisões, seja por parte de médicos, gestores ou clientes.

O Fluxo do Algoritmo

Vamos entender, de forma simplificada, como o algoritmo dos autores funciona e qual o papel de cada etapa no processo.

1. Coleta e Preparação dos Dados

Tudo começa com a obtenção e preparação dos dados. No caso do artigo, os autores usaram dados clínicos sobre doenças cardíacas. Mas os princípios de tratamento de dados são aplicáveis a qualquer contexto de negócios. As etapas incluem:

• Tratamento de valores ausentes: Dados faltantes podem comprometer a qualidade do modelo. Sejam substituídos pela média, moda ou outras técnicas, ou mesmo eliminados, isso precisa ser feito com cuidado.

• Codificação de variáveis categóricas: Muitos modelos de aprendizado de máquina só funcionam com dados numéricos, então variáveis categóricas precisam ser transformadas, com técnicas como One-Hot Encoding.

• Normalização ou padronização: Variáveis com escalas diferentes (como renda anual e idade) precisam ser ajustadas para facilitar o trabalho do algoritmo.

• Divisão dos dados: Sempre dividimos os dados em treinamento e teste para garantir que possamos avaliar o modelo com dados que ele ainda não viu.

• Balanceamento de classes: Quando as classes estão desbalanceadas (por exemplo, muito mais clientes inadimplentes do que adimplentes), técnicas como o SMOTE podem ser utilizadas para gerar amostras sintéticas da classe minoritária e garantir que o modelo seja treinado de forma equilibrada.

2. Seleção dos Modelos de Ensemble

Os autores do artigo optaram por três modelos de ensemble, que são conhecidos por sua robustez e capacidade de reduzir o risco de overfitting:

• Random Forest: Um conjunto de várias árvores de decisão, construídas a partir de amostras aleatórias dos dados. Cada árvore contribui com uma previsão, e o modelo final toma uma “decisão coletiva”. Isso reduz a variação e melhora a precisão.

• AdaBoost: Este modelo ajusta várias iterações de classificadores simples, atribuindo mais peso aos exemplos mal classificados a cada nova rodada. Ele se “adapta” aos erros, ajustando-se para melhorar a precisão.

• XGBoost: Uma implementação otimizada de Gradient Boosting, que se destaca pela eficiência e pelo desempenho elevado. É amplamente utilizado em competições de machine learning devido à sua capacidade de lidar com grandes volumes de dados e produzir previsões precisas.

3. Otimização de Hiperparâmetros com Otimização Bayesiana

A cereja do bolo nesta abordagem é a Otimização Bayesiana, que torna o processo de ajuste de hiperparâmetros mais inteligente. Em vez de usar o grid search tradicional, que testa várias combinações de parâmetros de forma exaustiva, a Otimização Bayesiana modela a função objetivo (neste caso, a AUC) e decide de forma eficiente quais conjuntos de parâmetros testar a seguir. Isso economiza tempo e recursos computacionais.

4. Avaliação e Seleção do Modelo

Depois que os modelos são otimizados, eles são avaliados em métricas como:

• AUC (Área Sob a Curva ROC): Mede a capacidade do modelo de distinguir entre classes positivas e negativas.

• F1-Score: A média harmônica entre precisão e recall, usada principalmente quando os dados estão desbalanceados.

• Precisão e Recall: Essas métricas medem a proporção de predições corretas e a capacidade do modelo de encontrar todas as instâncias da classe positiva.

Os autores ajustaram o limiar de decisão (threshold) para otimizar as métricas de acordo com o contexto, um passo importante quando o equilíbrio entre precisão e recall é crucial.

5. Interpretabilidade com Valores SHAP

Uma vez escolhido o melhor modelo, os autores usaram os valores SHAP (SHapley Additive ExPlanations) para explicar as previsões. O SHAP nos ajuda a entender a importância de cada característica, atribuindo um valor específico para a contribuição de cada variável nas previsões do modelo.

Por que isso é importante? Porque em muitos casos, como em diagnósticos médicos ou decisões empresariais, o “porquê” é tão importante quanto o resultado em si. Saber que uma variável como “pressão arterial” influenciou fortemente a decisão pode ser crucial para validar o resultado e tomar decisões informadas.

Por Que Essa Abordagem É Importante?

Esse tipo de abordagem, que combina precisão com interpretabilidade, é crucial em muitos contextos. Modelos eficientes são ótimos, mas se você não souber explicar suas decisões, pode perder a confiança de seus stakeholders. Isso é especialmente relevante em setores como saúde e finanças, onde a transparência é uma exigência.

Além disso, o uso da Otimização Bayesiana ajuda a economizar tempo e recursos, ajustando os modelos de maneira eficiente e inteligente. Isso significa menos horas gastas testando combinações de hiperparâmetros e mais tempo para analisar e melhorar os resultados.

Adaptando para Outros Contextos

Embora o foco do artigo seja a previsão de doenças cardíacas, os mesmos princípios podem ser aplicados em vários outros cenários de negócios:

• Análise de risco de crédito: Prever a probabilidade de inadimplência de clientes.

• Detecção de fraudes: Identificar transações suspeitas em tempo real.

• Previsão de churn: Antecipar quais clientes estão propensos a abandonar o serviço.

• Classificação de leads: Priorizar potenciais clientes com maior probabilidade de conversão.

A estrutura do algoritmo permanece a mesma; o que muda são os dados e, possivelmente, algumas nuances no pré-processamento ou nas métricas de avaliação.

Um Vislumbre do Código

Para ilustrar como isso se traduz em código Python, vamos dar uma olhada em um esboço simplificado da implementação:

# Importação das bibliotecas necessárias
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from skopt import BayesSearchCV
import shap
from sklearn.datasets import fetch_openml
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt

# Carregamento e preparação dos dados com as_frame=False
data = fetch_openml(name='heart', version=1, as_frame=False)

# Definir os nomes das colunas conforme documentação do dataset
feature_names = [
    "age", "sex", "cp", "trestbps", "chol", "fbs", "restecg", "thalach", 
    "exang", "oldpeak", "slope", "ca", "thal"
]

# Converta a matriz esparsa para uma matriz densa e crie o DataFrame
X = pd.DataFrame(data.data.toarray(), columns=feature_names)  # Converte para DataFrame com os nomes corretos
y = pd.Series(data.target)

# Certifique-se de que a variável-alvo é binária (0 ou 1)
y = np.where(y > 0, 1, 0)  # Converte todas as classes maiores que 0 para 1

# Divisão em treino e teste
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)

# Normalizar as variáveis numéricas
# Ajuste para lidar com dados esparsos, com with_mean=False
scaler = StandardScaler(with_mean=False)
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# Definição do espaço de hiperparâmetros para o Random Forest
param_space = {
    'n_estimators': (10, 200),
    'max_depth': (1, 20),
    'min_samples_split': (2, 10)
}

# Otimização Bayesiana
bayes_search = BayesSearchCV(
    RandomForestClassifier(random_state=42),
    param_space,
    n_iter=100,
    scoring='roc_auc',
    cv=5,
    n_jobs=-1,
    random_state=42
)

# Ajuste do modelo
bayes_search.fit(X_train, y_train)
best_model = bayes_search.best_estimator_

# Avaliação do modelo
y_pred = best_model.predict(X_test)

# Calcular a acurácia e exibir a matriz de confusão
accuracy = accuracy_score(y_test, y_pred)
cm = confusion_matrix(y_test, y_pred)

print(f"Acurácia: {accuracy:.4f}")
print("Matriz de Confusão:")
print(cm)

# Verifique se X_test é uma matriz densa
X_test_dense = pd.DataFrame(X_test, columns=feature_names)

# Interpretabilidade com SHAP
explainer = shap.TreeExplainer(best_model)
shap_values = explainer.shap_values(X_test_dense)

# Pegando os valores SHAP apenas para a classe 1 (classe positiva)
shap_values_class_1 = shap_values[:, :, 1]

# Gerar o gráfico com os valores SHAP para a classe positiva
shap.summary_plot(shap_values_class_1, X_test_dense, show=False)

# Salvar o gráfico gerado em PNG
#plt.savefig('shap_summary_plot.png', format='png', dpi=300)

# Exibir o gráfico (se desejar vê-lo na tela também)
plt.show()

Aqui, aplicamos a Otimização Bayesiana para encontrar os melhores hiperparâmetros para um modelo de Random Forest e usamos o SHAP para interpretar suas previsões.

from sklearn.metrics import accuracy_score, confusion_matrix

# Convertendo as probabilidades em classes binárias usando um threshold (por exemplo, 0.5)
y_pred = (y_pred_proba >= 0.5).astype(int)

# Cálculo da acurácia
accuracy = accuracy_score(y_test, y_pred)
print(f"Acurácia: {accuracy:.4f}")

# Geração da matriz de confusão
cm = confusion_matrix(y_test, y_pred)
print("Matriz de Confusão:")
print(cm)

Acurácia: 0.8642
Matriz de Confusão:
[[39  6]
 [ 5 31]]

Comentando as Figuras e Resultados

Para complementar nossa compreensão inicial, vamos dar uma olhada rápida nas figuras e nos resultados obtidos pelo modelo. Não se preocupe se alguns conceitos ainda não estiverem claros; nos próximos capítulos, iremos explorar cada um deles em detalhes.

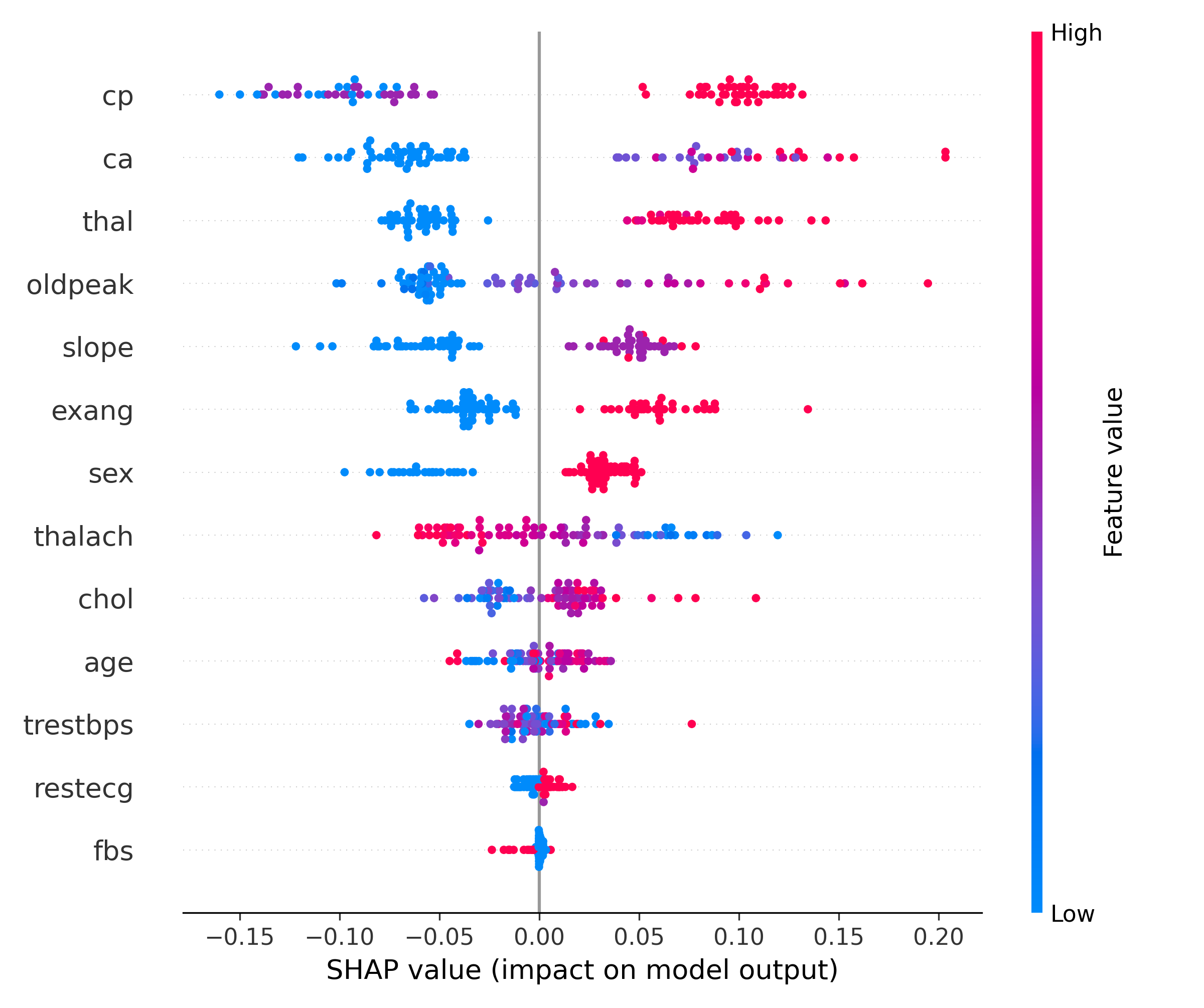
Figura 1.1: Interpretabilidade com SHAP

A Figura 1.1 apresenta um gráfico de resumo dos valores SHAP, que nos permite visualizar a importância de cada característica no modelo. As cores e posições dos pontos fornecem insights sobre como cada variável afeta as previsões. Embora não entremos em detalhes agora, este gráfico é fundamental para entender a interpretabilidade do modelo, e iremos explorá-lo aprofundadamente mais adiante.

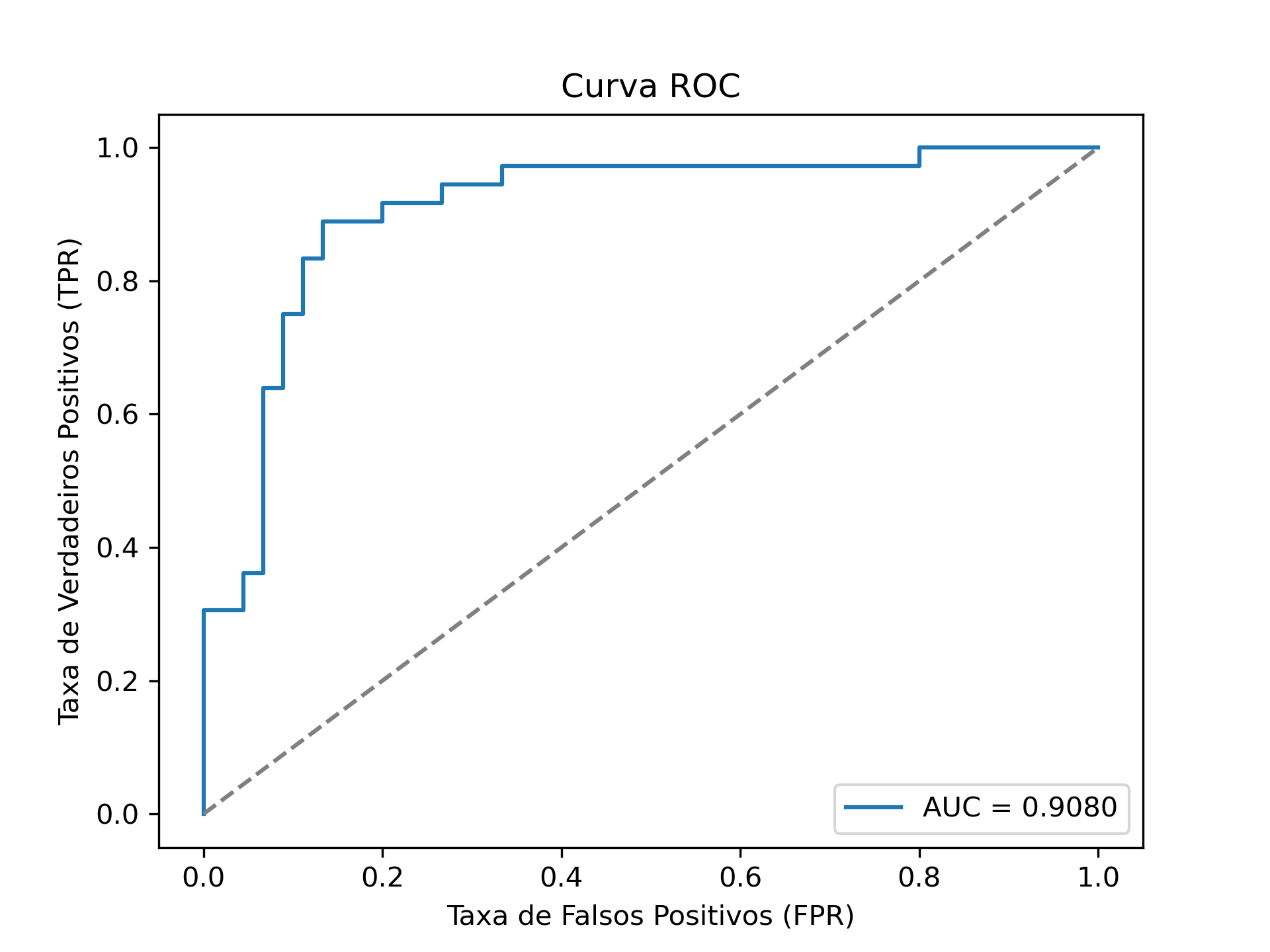
Figura 1.2: Curva ROC

A Figura 1.2 mostra a Curva ROC (Receiver Operating Characteristic) do nosso modelo. Esta curva é uma ferramenta poderosa para avaliar a capacidade do modelo em distinguir entre as classes positivas e negativas em diferentes limiares de decisão. A proximidade da curva ao canto superior esquerdo indica um desempenho robusto. Nos capítulos futuros, iremos dissecar esta curva para entender completamente o que ela revela sobre a performance do modelo.

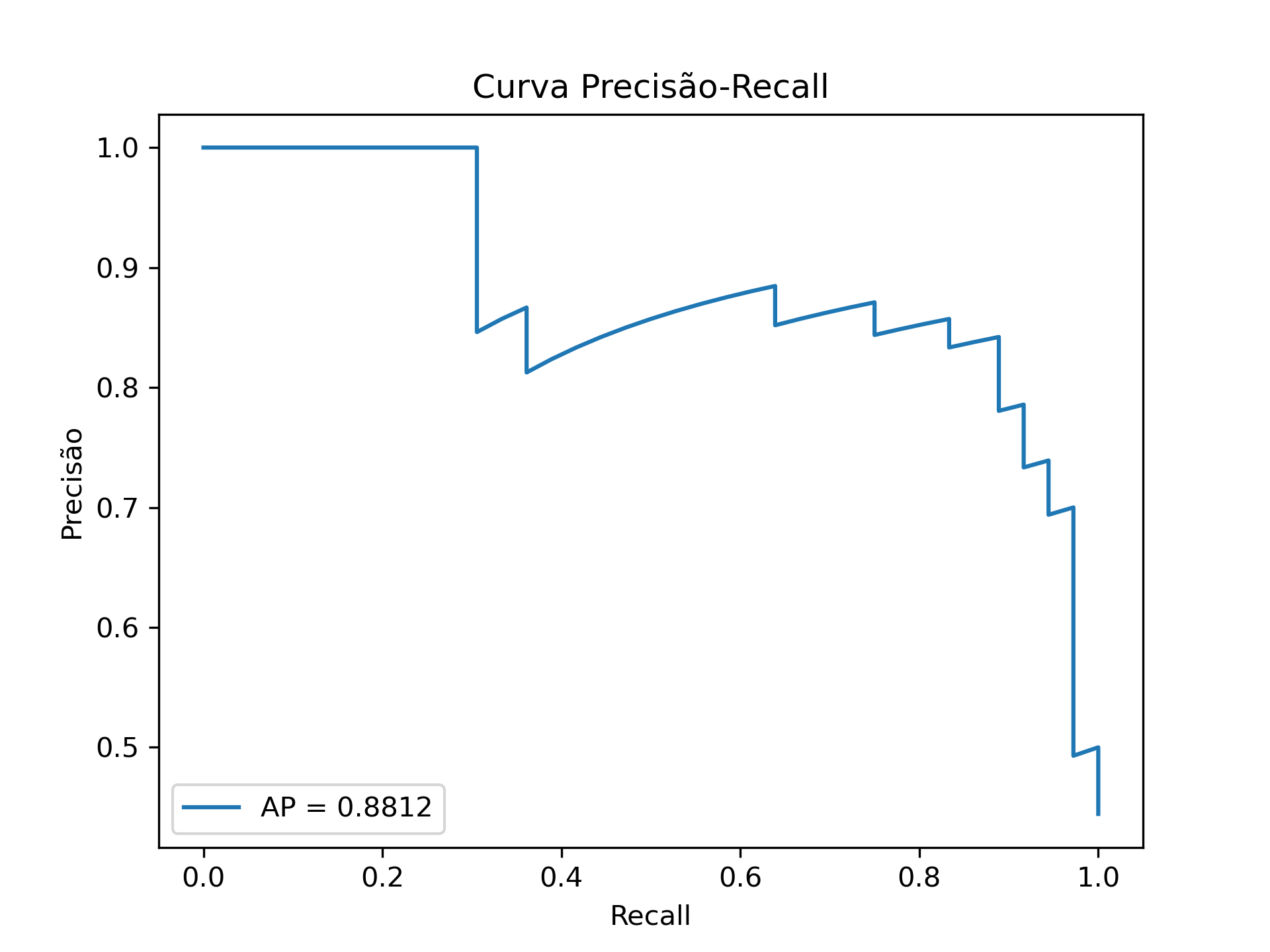
Figura 1.3: Curva Precisão - Recall

A Figura 1.3 apresenta a Curva Precisão-Recall, que é especialmente útil quando lidamos com conjuntos de dados desbalanceados. Esta curva nos ajuda a encontrar o equilíbrio ideal entre precisão e recall, permitindo otimizar o modelo de acordo com as necessidades específicas do negócio. Fique tranquilo, iremos explorar como interpretar e utilizar esta curva nos próximos capítulos.

Resultados de Desempenho do Modelo

Além das visualizações geradas com SHAP e as curvas de ROC e Precisão-Recall, obtivemos métricas quantitativas que ajudam a avaliar o desempenho do modelo:

• Acurácia: 0.8642

• Matriz de Confusão:

    [[ 39   6]
     [  5 31]]

A acurácia indica que nosso modelo está correto em aproximadamente 86% das previsões, o que é um resultado promissor. A matriz de confusão nos fornece uma visão detalhada das classificações verdadeiras e falsas para cada classe:

• Verdadeiros Positivos (TP): 39 casos em que o modelo previu positivamente e estava correto.

• Verdadeiros Negativos (TN): 30 casos em que o modelo previu negativamente e estava correto.

• Falsos Positivos (FP): 6 casos em que o modelo previu positivamente, mas estava incorreto.

• Falsos Negativos (FN): 5 casos em que o modelo previu negativamente, mas estava incorreto.

Este balanço entre TP, TN, FP e FN é crucial para entender as implicações práticas do modelo, especialmente em contextos onde os custos de falsos positivos e falsos negativos são diferentes. No decorrer do livro, iremos analisar profundamente estes resultados para extrair insights valiosos e aprimorar ainda mais o modelo.

Este é apenas um esboço para dar uma ideia geral. Nos próximos capítulos, vamos aprofundar cada etapa, adicionando detalhes e explicações para que você possa replicar e adaptar a abordagem ao seu contexto específico.

Neste capítulo, exploramos em detalhes o algoritmo proposto pelos autores do artigo que inspirou nossa jornada. Entendemos como a combinação de modelos de ensemble otimizados e interpretabilidade através de valores SHAP pode criar soluções poderosas e aplicáveis a diversos problemas de negócios.

A chave aqui é a adaptabilidade. Embora o caso de uso original seja a previsão de doenças cardíacas, os princípios e técnicas podem ser aplicados a uma ampla gama de desafios. Compreender o fluxo do algoritmo e os motivos por trás de cada etapa nos prepara para colocar tudo isso em prática.

No próximo capítulo, vamos arregaçar as mangas e mergulhar no código. Vamos apresentar a implementação completa, explicando cada linha em detalhes para que você possa entender não apenas o “como”, mas também o “porquê” de cada decisão.

Prepare seu ambiente de desenvolvimento e até lá!

Posts

• Sep 25, 2024

  Capitulo 01

• Sep 25, 2024

  Apresentacao

subscribe via RSS